零知识证明由于其本身陡峭的入门学习曲线,往往被初学者称为moon math。为了平缓学习曲线,减轻入门压力,babysnark[1]应运而生,本文将作为babysnark原理部分的一个解读版,帮助你更好的理解snark背后的一些基本概念和直觉。在阅读本文之前,希望你已经读过# 从零开始学习 zk-SNARK系列的前4部分,对包括有限域、椭圆曲线等相关知识有一个基本的了解。
R1CS
比如我们有这样一段程序:
def qeval(x):
y = x**3
return x + y + 5
我们知道程序执行实际上是CPU中的乘法门和加法门组合运算得到的。那么上面的程序可以看成是类似是下面的这个图,有一些输入变量和中间运算过程,最后得到输出。
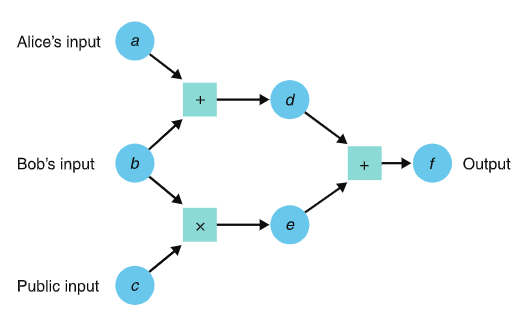
sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5
为什么我们输入一定要写成两个变量而不能是三个或者多个变量呢?具体限制原因可以从限制运算[3]中找到答案。简单来说,多项式的算数性质有在某一个具体的点上,左操作数和右操作数相乘等于输出结果。而这个约束特点使得每一次输入只能是两个数的形式,如果一次有多个变量作为输入,可以分别将其拆分成两两组合。
有了这样的直觉之后我们可以来看一下R1CS(Rank 1 constraint system)的具体定义:
给定三个m行n列的矩阵 , 和一个 维向量 定义了一组m个方 程,每个方程的形式如下:
其中 , ·表示矩阵和向量的乘积, 表示 的第 个元素。 等价地,我们可以使用Hadamard积(逐元素相乘)来表示整个系统:
其中○表示Hadamard积。
其中A可以看作是左操作数的全局结果的矩阵表示,B可以看成是右操作数全部结果的矩阵表示。C是运算结果的全部结果的矩阵表示。接下来让我们一步一步将上述4个等式转变成矩阵的Hadamard积的形式。
假设我们将上述4个等式的输入输出变量按如下顺序排列:
'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'
那么对于第一个等式
sym_1 = x * x
左操作数a,右操作数b和最后结果c可以分别表示成如下向量形式
a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]
然后向量和上述6个变量相乘,就可以还原出第一个等式了。类似的,我们对等式2,3,4做同样的处理,最终可以得到矩阵A,B,C:
A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]
B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]
通过上述操作,我们就将一段程序转换成了R1CS的形式。
多项式插值
在实际的零知识证明系统中,不管具体零知识证明算法是哪种,总要有一个validator发出一个随机数作为challenge,然后prover接受这个随机数作为系统输入,然后返回一个输出结果。validator拿到输出结果看是否和挑战的随机数满足某种对应关系,如果满足就认为prover确实掌握了某种知识。为了实现validator可以找任意随机数,所以我们就有必要R1CS的约束关系转换成多项式的形式。
比如对于之前的矩阵A而言,如果竖着按列看,其实其对应的就是之前文中所说的6个变量
'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'
比如说,对于one变量而言,其在上述4个等式(即4种约束关系)中所组成的向量为
~one: [0, 0, 0, 5]
如果将其在笛卡尔坐标系中表示,假设我们选取x为1,2,3,4,那么该one所组成的多项式应该经过(1,0), (2,0), (3,0), (4,5)这4个点。在笛卡尔坐标系中,我们对于做操作数和有操作数以及结果的所有x坐标只要满足一致关系,他们所组成的多项式都满足R1CS约束关系。基于上述特点,我们可以对6个变量选定一致的x坐标然后使用插值的方式得到多项式的形式。下面是我们选定x坐标是1,2,3,4得到的矩阵A的多项式表示形式:
A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]
即one可以表示为:
其他变量的R1CS转换也同理。
QAP
这种转换成的多项式新形式称之为QAP(Quadratic Arithmetic Program)我们来看一下QAP的具体定义。
定义(QAP): 一个在域 上的二次算术程序 包含三种 多项式:
- 其中 ,以及一个目标多项式 。
假设 是一个算术程序,它以 个 的元素为输入并输出 个元素,总共有 个I/O元素。那么,当且仅当存在系数 使得 可以整除 时, 是 的输入和输出的有效赋值,其中:
布尔电路
通常情况下一般的通用snark算法使用的是QAP来去表示程序,但如果程序是一些特殊问题,比如输入程序可以表示为布尔电路,那么QAP实现就可以更加简单一点。首先我们来看一下布尔电路的特点:
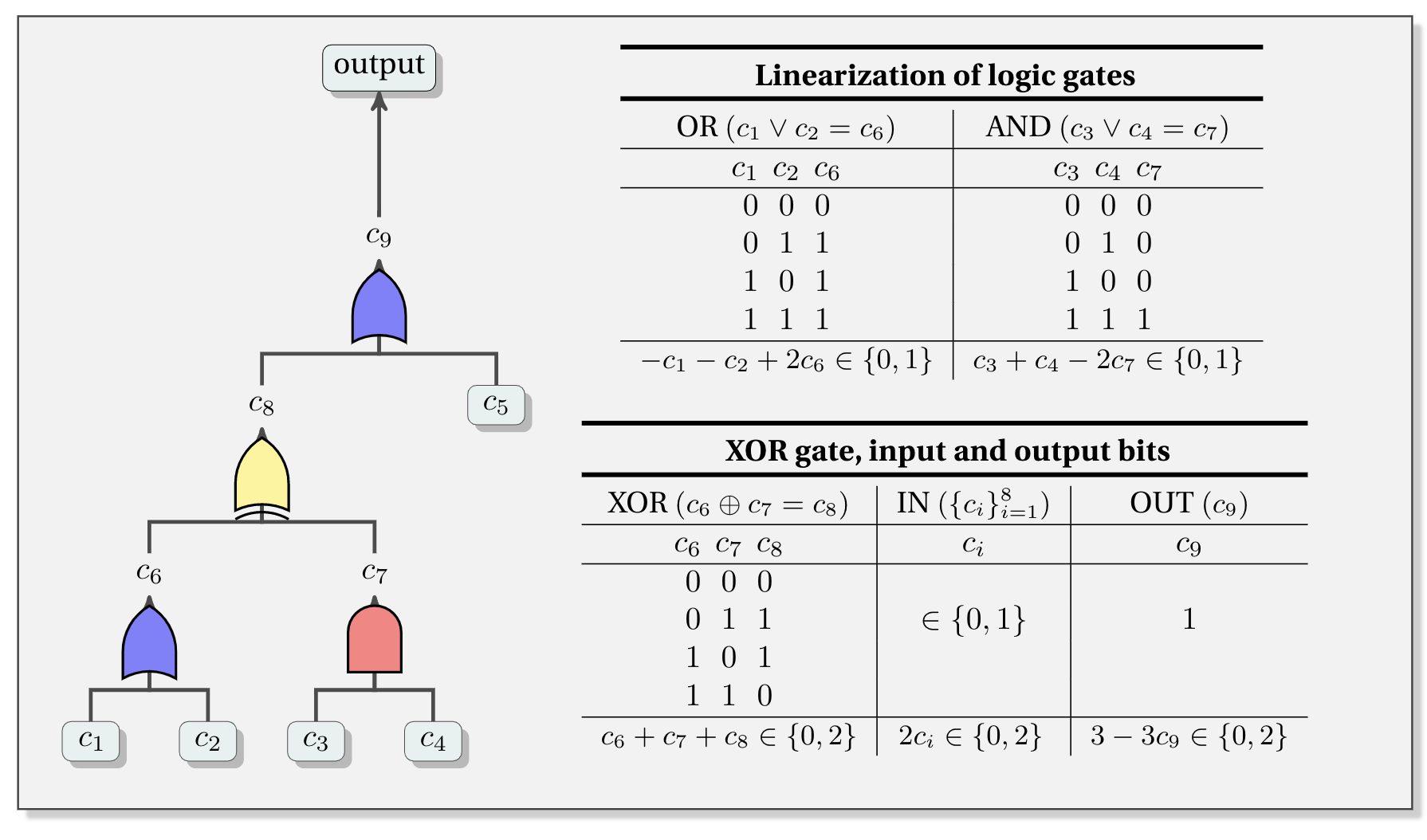
从图中可以看到不管是哪一种的门,最终的输出结果一定是落在[0, 2]区间之内。具体来说:任何一个2输入的二进制门电路 ,其中输入为 ,输出为 ,都可以使用门电路的输入和输出的仿射组合 来指定,当输入输出满足门电路的逻辑规范时,它只能取两个值, 或 。这导致了一个等效的单一的“平方”约束 。
SSP
根据上述布尔电路的特点,一般的QAP约束在布尔电路中就转换成了SSP(Square Span Program)约束。我们来看一下SSP的具体定义:
定义(SSP):在域 上的一个方形跨度程序(SSP)是由 个多项式 和一个目标多项式 组成的元组,使得对所有 ,都有 。我们说方形跨度程序SSP的大小为 ,并且度数为 。当且仅当存在 ,使得 能够整除 时,我们称SSP接受输入 ,其中:
我们说SSP校验了布尔电路 ,如果它仅接受那些满足 的输入值 。
再进一步,我们可以根据SSP而具体的布尔电路构造方形约束系统(Square Constraint System)。我们首先来看一下SCS的定义:
定义SCS: 方形约束系统由一个矩阵 定义。如果满足以下条件
其中 表示Hadamard(逐元素)乘积,那么向量 是此系统的解。我们也将 写为 。
我们可以看一个具体的例子,比如我们有3个布尔元素分别是 : 对于布尔元素而言,比如说 要么为 0,要么为 1。注意到
这意味着 ,从而推导出 。其他元素也是同理。对于 为
综合上述内容,一个包括上述导线和门的方形约束程序将采取以下形式:
babysnark
介绍了这么多,终于到babysnark了。babysnark是对布尔电路所构造的一种snark。相比于QAP而言,SSP更简单,所以实现整个snark所需的约束也更少。具体来说一共有两个约束,第一个是SSP约束:
不需要做太多解释,第二个约束是线性约束:
这个和babysnark具体设计有一些关系。 的值是由prover直接计算的,而 的值来自于setup阶段。设置线性约束的目的是确保 确实是由同一线性多项式计算出来的,防止prover作弊,恶意构造 而不是赖在setup所提供的随机challenge构造的 ,最终破坏SSP约束。因为prover最后输出证明的时候同时提供了 和 在verify阶段添加 是为了防止证明者输出特别恶意构造的 B=YV,所以再做一次线性约束。
babysnark的随机挑战采用的是 的形式,该构造形式的安全保证来自q-DLOG 假设。q-DLOG 假设确保即使敌手可以在多个点上观察到多项式的值,他们也无法从多项式的结构中提取任何信息。
至此,我们对babysnark的原理部分做了详细的探讨。希望通过深入浅出的方式介绍这一简易的snark,能为你的零知识证明学习之旅提供坚实的基石。
Reference
[2] quadratic-arithmetic-programs-from-zero-to-hero
[3] 从零开始学习 zk-SNARK(三)——从程序到多项式的构造
[4] zk-SNARKs: A Gentle Introduction